正多角形を媒介変数表示する：正弦波/矩形波/三角波/トロコイド/フーリエ級数/Epicycles

正多角形を媒介変数表示するためのメモ。
Python Matplotlibで円や図形を描くクラスはありますが、今回は数式を用いて図形を表示してみました。

正六角形の場合。
最終的には頂点座標だけではなく、任意の分解能で各辺を分割しつつ、外形線上の任意の点座標を求めます。


円の描画（基本）：
まずは基本として円の描画。図形クラスを使わずに数式で描画するには、

import numpy as np
import matplotlib.pyplot as plt

theta = np.linspace(0, np.pi*2, 100)
r = 1
x = r * np.cos(theta)
y = r * np.sin(theta)

plt.figure(figsize=(4, 4))
plt.axis('equal')
plt.grid()
plt.plot(x, y)

となります。thetaを0から2πまでの範囲で(x, y)をプロットすると以下のグラフ。

np.linspace(0, np.pi*2, 100)なので、厳密には正99角形を描いていることになります。正100角形にするには、np.linspace(0, np.pi*2, 101)。つまり正n角形を描くにはnp.linspace(0, np.pi*2, n+1)にします。

また、thetaを横軸、yを縦軸にすれば以下のような正弦波になります。

n角形の頂点数による表示：

以下は正方形（n=4）の場合。plt.scatter(x, y)を使うと正方形なら4つの頂点だけがプロットされます。

n = 4
theta = np.linspace(0, 2*np.pi, n+1)
r = 1
x = r * np.sin(theta)
y = r * np.cos(theta)

plt.figure(figsize=(4, 4))
plt.axis('equal')
plt.grid()
plt.scatter(x, y)

コード内ではxとyをsinとcosで求めていますが（図形の向きを合わせるためxにsinを用いています）、複素数を使うと以下のようになります。虚数は通常iですがPythonでは1jになります。xとyはvの実部realと虚部imagに対応しています。

v = np.exp(1j * theta)

x = v.real

y = v.imag

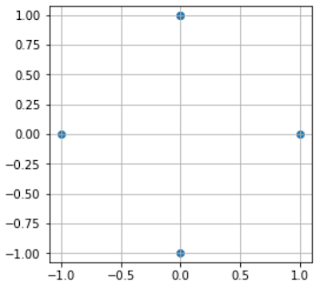
正方形なので4点ありますが、コード上では以下のplt.plot()で線を引くために座標(1, 0)には2点重なっており合計で5点あります。

そしてplt.plot(x, y)で各頂点を線でつなくと以下のような正方形が描画されます。

この場合、連続値で線を描いているわけではないので、辺上の任意の点座標を数式によって求めていません。連続値を用いて角を持った図形やグラフを描くにはどうすればよいか？ということについて以下に続きます。

正弦波を矩形波へ変換：

正弦波は滑らかな曲線ですが、正弦波を無数に重ね合わせる（無限フーリエ級数）と矩形波に近づいていきます。

数式的には、nを正の奇数として（n=1, 3, 5 ...）、

y = 4/π * {1/1*sin(1*θ) + 1/3*sin(3*θ) + 1/5*sin(5*θ) + ... + 1/n*sin(n*θ)}

となります。

n=10までを重ね合わせるコードは以下 。分解能は100。

theta = np.linspace(0, np.pi*2, 101)
n = 10
sq = 4 / np.pi * sum([np.sin(n*theta) / n for n in range(1, n, 2)]) 

ちなみに、n=10とn=50までの重ね合わせをグラフにすると、

青が元の正弦波、黄色がn=10、緑がn=50のときの矩形波。まだ矩形波としては不完全。

n=200まで重ね合わせるとかなり角がでてきます。無限級数なので数が大きいほどより正確な矩形波に近づいていきます。

上図は横軸がθ（角度）、縦軸がyの値なので、これを元に(x, y)のグラフを表示させると以下のような正方形になります。

今回はグラフの分解能を100にしていますが、分解能を上げるほどより近似していきます。

もう一つの方法：

フーリエ級数の式はやや面倒なので、もう少し簡単にコーディングすると以下になります。

sq = np.sin(theta)
for _ in range(10):
    sq += np.sin(sq)
sq /= np.pi

正弦波の式に正弦波を自己代入して合算し（今回は10回自己代入）最後にπで割っています。結果のグラフは以下。

三角波：

次は三角波です。数式的には矩形波のように奇数の級数がでてきますが、一つおきにプラスマイナス反転するので少し複雑です。

tr = 8/π² * sin{1/1²*sin(1*θ) - 1/3²*sin(3*θ) + 1/5²*sin(5*θ) - 1/7²*sin(7*θ) + ...}

上式のsin{...}内の偶数番目（2²など）の項をゼロにして奇数番目を一つおきにプラスマイナス反転させるには、

sin(n*π/2)

を使うと、n=1, 2, 3, 4, 5 ...　のとき、

1, 0, -1, 0, 1, 0, -1, 0, 1, ...

という値を返します。この式を使ってコーディングすると（n=100まで）、

tr = 8 / np.pi**2 * sum([1/k**2 * np.sin(k*np.pi/2) * np.sin(k*theta) for k in range(1, 101)])

となり、これを描画すると以下。

赤が三角波、青が元の正弦波、横軸はθ、縦軸はy値。
また(x, y)をグラフ表示すると以下。

トロコイド：
車輪を地面上で転がしたときに、車輪上の任意の点が動く軌跡。

wiki:Trochoidより

車輪の半径をR、車輪上の任意の点の半径をr、回転角をthetaとしたとき、

theta = np.linspace(0, np.pi*2, 100)
R = 1
r = 1
x = R*theta - r*np.sin(theta)
y = R - r*np.cos(theta)

R=rのときサイクロイドと呼び、(x, y)の軌跡は以下。

横軸：x、縦軸：y

外トロコイド（Epitrochoid）：
上記トロコイドにおいて、地面の代わりに円の外側を回る車輪上の任意の点の軌跡。

wiki：「トロコイド」より

地面の代わりとなる円の半径をR、車輪の半径をr、車輪上の任意の点の半径をn、回転角をthetaとしたとき、

R = 1
r = 1/4
n = 1/4
theta = np.linspace(-np.pi, np.pi, 100)

x = R * np.cos(theta)
y = R * np.sin(theta)

X = (R + r) * np.cos(theta) - n * np.cos((R + r) / r * theta)
Y = (R + r) * np.sin(theta) - n * np.sin((R + r) / r * theta)

r=nのとき外サイクロイドと呼び、(X, Y)の軌跡は以下。

青が半径R=1の固定された円、黄色がその上を転がる半径r=1/4でn=rの軌跡。r=1/4のため青い円の外周を4分割する。r=1/3にすれば3分割、r=1/5にすれば5分割となる。n=0のとき黄色い軌跡は半径R+rの円になる。


内トロコイド（Hypotrochoid）：
外トロコイドとは逆に固定円（青い円）の内側を回るときの軌跡。

R = 1
r = 1 / 4
n = 1 / 4
theta = np.linspace(0, np.pi*2, 100)

x = R * np.cos(theta)
y = R * np.sin(theta)

X = (R - r) * np.cos(theta) + n * np.cos((R - r) / r * theta)
Y = (R - r) * np.sin(theta) - n * np.sin((R - r) / r * theta)

r=nのとき内サイクロイドと呼び、(X, Y)の軌跡は以下。

青が半径R=1の固定された円、黄色がその内側を転がる半径r=1/4でn=rの軌跡。r=1/3で3分割、r=1/5で5分割の軌跡になる。n=0のとき黄色い軌跡は半径R-rの円になる。

r=1/4、n=1/10にすると以下。

r=1/4なので正方形に近い軌跡になりますが、角が丸くなってしまいます。


角が丸くならないようにする：
「いかに丸くならない角と直線で多角形を描くことができるか？」という方法についてです。

先ほど、正弦波を無限フーリエ級数的に重ね合わせると直角と直線に近似した矩形波を描くことができましたが、トロコイドでは角をシャープにすれば辺が曲線になってしまい、辺を直線に近づければ角が丸まってしまいます。そこで、もう少しシンプルに円の公式を利用して直角に近似する方法を試してみました。

円の公式：x**2 + y**2 = r**2なので、y = (r**2 - x**2)**(1/2)として、円の半径r=1、xの分解能を100とすると、

n = 2
r = 1
x = np.linspace(-r, r, 101)
y = (r**n - x**n)**(1/n)

xに対するyが求まり、これを表示すると、

このような円弧になります。
さらにn=4にするとx**4 + y**4 = r**4となり、y = (r**4 - x**4)**(1/4)の場合は、

やや角ばってきます。
xⁿ + yⁿ = rⁿのnを大きくするほど角がでてきます。
さらにn=100にすると、以下のように直角に近づいていきます。

n=2のとき円弧で、nが大きくなるほど四角くなっていきます。
この場合、xが-1から1までの間を分解能100で描いているので、より連続値に近い表現方法になりますが、plt.scatter(x, y)で点描してみると以下のようになってしまいます。

y=1の水平な辺は連続する点群で描画されていますが、左右の縦の辺はそれぞれ2点で表現されているので、連続値による表現にはなっていません。これはxを媒介変数としているので仕方ありませんが、やはり中心角となるθを媒介変数にしたほうがよさそうです。


中心角θを媒介変数として多角形を描く：
多角形の頂点を求めて辺をつないで描くのではなく、任意の中心角θにおける多角形の外形線の(x, y)座標を求める方法についてです（こちらを参考にしました）。

以下がコードです。n=3のときに正三角形を描きます（正n角形）。

n = 3
resolution = n * 10
theta = np.linspace(0, np.pi*2, resolution+1)

r = 1 / np.cos(theta % (2*np.pi/n) - np.pi/n)
x = r * np.sin(theta)
y = r * np.cos(theta)

plt.figure(figsize=(4, 4))
plt.axis('equal')
plt.plot(x, y, alpha=0.5)
plt.scatter(x, y, s=10, c='r')
for i in range(len(theta)):
    plt.plot([0, x[i]], [0, y[i]], c='gray', lw=0.5)
    
plt.figure(figsize=(4*np.pi, 4))
plt.grid()
plt.axis('equal')
plt.plot(theta, r)

頂点座標だけではなく、任意の中心角θに対する辺上の点座標(x, y)を求めることができます。
resolutionは中心角0〜2πにおける分解能です。頂点を含めるためnの倍数にしています。rは角度θにおける中心(0, 0)からの距離です。rとθが分かればsinとcosで(x, y)の座標を求めることができます（図形が90度ずれるので、xにsin、yにcosを使用しています）。

n=3、分解能30（1辺を10分割）の場合。赤点が分解能30における辺上の点。

n=4、分解能40の場合。

横軸：θ（0から2π）、縦軸：rのプロット。つまり、中心(0, 0)からの辺上の任意の点までの距離。正方形の場合このような波型の線が4つできます。

n=5 、分解能100の場合。分解能を上げれば線画に近づいていきます。

この方法では中心角θを分解能に応じて均等に分割しているためプロットされる点は辺を均等に分割してはいませんが、n角形の頂点だけではなく辺上の点座標を求めることができます（辺を均等に分割する場合は以下のEpicycleの方法で）。


多角形を歪ませて表示：
前述の方法で多角形における頂点以外の任意の点座標も求めることができたので、多角形そのものを歪ませてみます。
正方形を例として、回転、伸縮、湾曲させてみます。

n = 4
resolution = n * 10
theta = np.linspace(0, np.pi*2, resolution+1)

r = 1 / np.cos(theta % (2*np.pi/n) - np.pi/n)
theta += np.pi/n # tilted at 45 degrees
x = r * np.sin(theta)
y = r * np.cos(theta)

#plt.figure(figsize=(4, 4))
plt.axis('equal')
plt.plot(x, y, alpha=0.5)
plt.scatter(x, y, s=10, c='r')

plt.plot(x*1.2, y) # yellow line

y1 = 1/4 * x**2
plt.plot(x+0.3, y+y1+0.1) # green line

歪ませた結果は以下。

もともと正方形が45度傾いて菱形になっていたので、辺を垂直水平にあわせました。
黄色は横幅を1.2倍したもの。
緑はy=1/4*x**2の放物線を加えて座標(0.3, 0.1)ずらしたもの。
頂点以外の点もプロットされているので全体的に湾曲します。


Epicycle：フーリエ級数で正多角形を描く：
もう一つの方法として、Epicycleという複数の回転軸を連結させて図形を描く方法。
矩形波で複数の波形を重ねたように、周期性のある回転軸をフーリエ級数的に足し合わせて、単純な円から複雑な図形に変換していきます。
基本の数式は、

e^iθ= cosθ + i*sinθ

eはエクスポネンシャル、iは虚数、θは任意の角度のとき、複素平面上で実部が横軸、虚部が縦軸となり、

e^iπ = -1：座標(1, 0)から反時計回りにπ（180度）回転し座標(-1, 0)に移動
e^2iπ = -1：座標(1, 0)から反時計回りにπ（360度）回転し座標(1, 0)に移動
e^iπ/2 = i：座標(1, 0)から反時計回りにπ/2（90度）回転し座標(0, i)に移動
e^-iπ = -1：座標(1, 0)から時計回りにπ（180度）回転し座標(-1, 0)に移動
2e^iπ = -2：座標(2, 0)から反時計回りにπ（180度）回転し座標(-2, 0)に移動

という関係になります。つまり複数の回転軸を持つ円を重ね合わせる際に、円の大きさや回転角、回転する向きを各係数で指定し任意の座標へ移動できます。

例えば、正三角形（n=3）を描画する場合は、係数をcとして、Σは-∞から∞までの範囲で、

R = Σ(1/c² * e^ciθ)

となるようです。
求められるRは複素数で、Rの実部をx成分、Rの虚部をy成分とした(x, y)座標に点がプロットされます。
また、eの係数1/c²と指数部分にcがあり、係数cの配列をCとし、

C = [..., -8, -5, -2, 1, 4, 7, 10, ...]

1を基準として3ずつ加算した数列、また3ずつ減算した数列となります。

また正方形（n=4）であれば、

C = [..., -11, -7, -3, 1, 5, 9, 13, ...]

1を基準として4ずつ加算した数列、また4ずつ減算した数列となります。

正五角形（n=5）であれば同様に、

C = [..., -14, -9, -4, 1, 6, 11, 16, ...]

というように係数Cの配列は、1を基準としてnを加算、nを減算したものとなるようです。
仮に級数の個数をF=30としてコーディングすると、

F = 30
C = [1 + f*n for f in range(-F//2, F//2)]

という感じになります。nは任意の正n角形。
無限級数なので円の個数Fを多くするほど、より厳密な図形を描くことができます。

以下は全体のコード。

n = 4
resolution = n * 10
theta = np.linspace(0, 2*np.pi, resolution+1)
F = 4
C = [1 + f*n for f in range(-F//2, F//2)]
R = sum([1/c**2 * np.exp(c*1j*theta) for c in C])
ratio = sum([1/c**2 for c in C])

x = R.real / ratio
y = R.imag / ratio

plt.figure(figsize=(4, 4))
plt.grid()
plt.axis('equal')
plt.plot(x, y, alpha=0.5, )
plt.scatter(x, y, s=10, c='r')

n：正n角形
resolution：分解能（辺の分割数）
theta：分解能で分割した角度
F：フーリエ級数の数（数が大きいをほど描画精度が上がる）
C：フーリエ級数の係数
R：Epicycleの計算式、複素平面上のベクトル
x：ベクトルの実部をx成分に変換
y：ベクトルの虚部をy成分に変換
ratio：多角形頂点までの半径を1にするための比率

Fを下げると（F=4）描画精度も下がり角が丸くなってしまいます。

ということで、多角形の頂点だけでなく途中の点も各変数を調節しながら求めることができます。


もう一つの方法（分解能で分割）：
フーリエ級数を使わず、多角形の各辺を任意の分解能で分割する場合。

N = 4
theta = np.linspace(0, 2*np.pi, N+1)
V = np.exp(1j * theta) # V = np.cos(theta) + 1j*np.sin(theta)
Div = 10
P = np.array([(V[k+1] - V[k])*d/Div + V[k] for d in range(Div) for k in range(N)])

x = V.real
y = V.imag
vx = P.real
vy = P.imag

plt.figure(figsize=(4, 4))
plt.grid()
plt.axis('equal')
plt.plot(x, y, alpha=0.5)
plt.scatter(vx, vy, s=10, c='r')
plt.scatter(x, y, s=20, c='k')
plt.scatter(0, 0, s=50, c='k', marker='x')

Divは各辺を何分割するかという変数。その分割数から描く座標を求めています。
Vは正n角形のn個の点、Divは1辺の分割数、PがDivによって分割された点。


任意の中心角による辺上の点座標：
前述のような分割数で求めるのではなく、中心角を入力として辺上の点座標を求める方法。

def intersection(x1,y1,x2,y2,x3,y3,x4,y4):
    A = (x1-x2)*(y3-y4)-(y1-y2)*(x3-x4)
    B = (x1-x2)*(y3-y4)-(y1-y2)*(x3-x4)
    if A != 0 and B!= 0:
        px= ( (x1*y2-y1*x2)*(x3-x4)-(x1-x2)*(x3*y4-y3*x4) ) / A
        py= ( (x1*y2-y1*x2)*(y3-y4)-(y1-y2)*(x3*y4-y3*x4) ) / B
        return [px, py]

N = 4
theta = np.linspace(0, 2*np.pi, N+1)
R = np.exp(1j * theta)
x = R.real
y = R.imag

deg = np.deg2rad(70)
n = int(deg * N / (2*np.pi)) % N
px, py = intersection(0, 0, np.cos(deg), np.sin(deg), R[n].real, R[n].imag, R[n+1].real, R[n+1].imag)
        
plt.figure(figsize=(4, 4))
plt.grid()
plt.axis('equal')
plt.plot(x, y, alpha=0.5)
plt.plot([0, px], [0, py])
plt.scatter(px, py, s=10, c='r')

intersection()という二つの線分の交点を求める関数を用いています。中心からの半径となる線分と多角形の各辺との交点を求めるという手順です。
変数Nで正N角形を指定し、変数degに任意の角度（度数）を指定します。変数nは中心角radが正N角形のn番目の辺にあるという計算をしています。

N=4、deg=70度の場合。
np.deg2rad()は度からラジアンへ変換してくれます。

スバラシク実力がつくと評判のフーリエ解析キャンパス・ゼミ―大学の数学がこんなに分かる!単位なんて楽に取れる!

posted with amazlet at 19.10.24

馬場 敬之
マセマ
売り上げランキング: 254,052

Amazon.co.jpで詳細を見る

続き：フーリエ級数を用いて正多角形を描く（その２）

TSP LP with scipy.optimize.linprog

今回はscipyを使ってTSP（巡回セールスマン問題）を解いてみました。前回までのPulpのような最適化ソルバー/モデラーであれば0-1整数計画法（混合整数計画法）として計算可能でしたが、scipyの線形計画法の関数であるlinprogは整数計画法まではカバーされていないため、離散値（整数値）ではなく連続値として計算しなければいけません。Pulpを使ったほうがコーディングも楽だし処理も早いと思いますが、今回は敢えてscipyで可能かどうかという試みです。アルゴリズム的には基本的に前回と同じですが、今回は連続値を扱うのとscipyのフォーマットで書き直すため微妙に異なる点があります。データは前回同様TSPLIBのアメリカ48都市を用いることにします。

目的関数とベースの制約：

最小化する式は以下のようになります。

min: Σ(dist(i, j) * x(i, j))

s.t: sum(x(0, 1) + x(0, 2) + ... + x(0, 47)) = 2
     sum(x(0, 1) + x(1, 2) + ... + x(1, 47)) = 2
     ・・・
     sum(x(0, 47) + x(1, 47) + ... + x(46, 47)) = 2

とりあえず各都市において最低２本の経路が接続されていなければならないという条件を加えておきます。dist(i, j)は二都市間(i, j)における距離、x(i, j)は経路として採用された場合は1、不採用なら0になりますが、scipyの場合はこの値が連続値になるので0.0〜1.0の小数になります。

上記をscipy.optimize.linprogのフォーマットで書き直すと以下のようになります。

e = [(i, j) for j in range(num) for i in range(num) if i < j]
dist = [abs(XY[i] - XY[j]) for j in range(num) for i in range(num) if i < j]

A_eq = [[1 if n in (i, j) else 0 for (i, j) in e] for n in range(num)]
b_eq = [2] * num
bounds = [(0, 1)] * len(dist)
    
res = linprog(c=dist, A_eq=A_eq, b_eq=b_eq, bounds=bounds, method="revised simplex")

linprogの引数c=distは1次元配列でなければならないので、eとdistは二都市間(i, j)のマトリクスになりますが1次元配列として用意します。48*47/2=1128個の値を含んだ配列になります。

e：(i, j)の二都市を参照するための配列

dist：二都市間の距離を格納した配列

A_eq：各都市における二経路接続の制約マトリクス（二次元配列：1128x48）
b_eq：制約ベクター

bounds：x(i, j)の値の範囲（今回は0.0〜1.0の連続値）

この制約で一度答えを出してみます。methodはより正確なrevised simplexを用いることにします（そうしないとWarningが出る）。まず以下の方法でx(i, j)の値がそれぞれどのくらいになっているか見てみます。

plt.plot(list(range(len(dist))), res.x )

そうすると、以下のように1128通りあるx(i, j)は0か0.5か1.0（縦軸）になっています。

横軸はx(i, j)をx[n]のインデックス番号に変換した値です（n=0〜1127）。実際これを地図に落とし込むと以下のようになります。

赤い線がx(i, j)=0.5、グレーの線がx(i, j)=1.0です。今回はx(i, j)の値が0.0〜1.0の連続値になっているため、この段階では0.5と1.0の二種類の経路が混在しています（もしバイナリ設定が可能なPulpなどのライブラリを使えば0か1の表現になるのでもう少し簡単になるのですが）。

部分巡回路除去：

次の段階として、この状態から部分巡回路を選択して、その部分巡回路に追加の制約を与えます。まず目につくのが、右上にある7都市からなる部分巡回路と下部右寄りにある五角形の部分巡回路です。この段階で選択する部分巡回路の条件は、部分巡回路の都市数が全体の半数未満（48都市あるので24都市未満）でx(i, j)=1.0で構成されているもの（実際は0.5の経路群を含めても可）。複数ある場合は都市数が少ない方をターゲットとします。よって今回は下部右寄りにある五角形{2, 15, 21, 33, 40}を選択します。

ターゲットの部分巡回路の都市群をst_flat={2, 15, 21, 33, 40}として、以下の制約を追加して再度解きます。ST15[0]というのはこの都市群における経路群[(2, 21), (2, 33), (15, 21), (15, 40), (33, 40)]であり、st_flatというのは経路群を都市群に変換したものです。

st_flat = set(sum(ST15[0], ()))
A_ub = [[-1 if len({i, j} & st_flat) == 1 else 0 for (i, j) in e]]
b_ub = [-2]
res = linprog(c=dist, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds, method="revised simplex")

閉じている部分巡回路に対して部分巡回路外の都市と接続するように仕向けるための制約です。x(i, j)のiかjの一方が部分巡回路に属し、もう一方が属していない都市となるx(i, j)の組み合わせが2個以上という制約です。Pulpなどでの制約式としては以下のようになりますが（前回参照）、

sum([x(i, j) for (i, j) in e if len({i, j} & st_flat) == 1]) >= 2

scipy.optimize.linprogでは基本的に「<=」が使用されるため「>=」の場合はをマイナス反転するようです。よってA_ubにおいてx(i, j)が条件に従う場合は-1でそうでない場合は0という配列にしておきます（この部分が多少面倒）。またb_ubのほうにもマイナスをかけて「-2」にしておきます。

この結果、五角形の部分巡回路は以下のようにつながります。

次のターゲットは右上にある7都市の部分巡回路です。同様に制約を追加して解いていきます。

部分巡回路がない場合（接続数１）：

部分巡回路除去の手順を繰り返すと徐々に部分巡回路はつながっていき、以下のような状態になります。

この状態では分離した部分巡回路はありません。このようなひとつながりでありつつ巡回路としては不完全な状態のときには、条件を変えて次のターゲットを選ぶことにします。

今回の場合であれば、左側にある辛うじて一本の経路でつながっている7都市からなる都市群{3, 9, 23, 25, 34, 41, 44}を選択します。この経路はx(i, j)=0.5である赤い経路の都市群{9, 23, 25, 41, 44}とx(i, j)=1.0である{3, 25, 34, 44}と{9, 23}で構成されています。{41}の１箇所で全体に対してつながっているので、この都市群に最低でも二本の経路でつながるような制約を追加します。

似たような箇所として右上にある{5, 16, 18, 26, 27, 29, 35, 36, 42}も{35}の１箇所で辛うじてつながっています。このような１箇所でしか接続されていない都市群を探し出して二経路接続の制約を追加するというのが今回の手段になります。もちろんこれらの都市群の数は全体の都市数の半分未満の数でなければならないという条件と、もし複数ある場合は合計都市数の少ない方を選択するということにしておきます。

条件としては、

・x(i, j)=0.5だけで構成される部分巡回路を探す

・x(i, j)=0.5の部分巡回路に2箇所以上接続しているx(i, j)=1.0の部分巡回路/部分経路を足し合わせる

・足し合わせた都市群は全体都市数の半数未満でなければならない

という感じです。

この部分はかなり面倒な手続きになりますが、そのような都市群を探し出す関数を用意することにしました（あとで登場）。

よって、st_flat={5, 16, 18, 26, 27, 29, 35, 36, 42}に制約を与えると以下のようになります。

左側は部分巡回路として分離しましたがx(i, j)=0.5の赤い経路は消えてくれました。

以後は、これまでと同様に

・分離した部分巡回路（全体の半分未満の都市数からなる）

・分離した部分巡回路がない場合、１箇所でつながっている都市群

という条件で制約を追加していきます。

部分巡回路がない場合（接続数３以上）：

前述の手順を繰り返していると、以下のようなパターンもでてきます。

全体としてはつながっており、１箇所だけでつながっている部分もありません。次の条件としては、x(i, j)=0.5で構成される赤い部分巡回路で他の都市群に接続している部分が３箇所以上あるものを選び、他の都市群への接続数を２箇所以下に制約します。先ほどの方法同様、赤い部分巡回路に対して２箇所以上で接続しているx(i, j)=1.0の部分経路は赤い巡回路に足し合わせます。

具体的には、赤い巡回路{2, 13, 15, 22, 28, 33, 40}に着目します。x(i, j)=1.0である{33, 40}と{2, 15, 21}は、赤い巡回路{2, 13, 15, 22, 28, 33, 40}に対して２箇所で接続しているため、足し合わせて{2, 13, 15, 21, 22, 28, 33, 40}を今回のターゲットとします。

この都市群は{13}と{22}と{28}の3箇所において他の都市群とつながっているので、この接続数３を２以下に制約します。以下がこの部分のコード。

A_ub.append([1 if len({i, j} & st_flat) == 1 else 0 for (i, j) in e])
b_ub.append(2)

この制約で一旦解いてみると、以下のようになります。

分離した部分巡回路ができあがりましたが、赤い経路は消えてx(i, j)=1.0の部分巡回路だけになりました。

次に、最初の方法で右側の部分巡回路に二経路接続の制約を与えると、

部分巡回路がなくなってひとまとまりになります。これで最適解が得られました。

制約を与える手順：

今回は0.5の経路と1.0の経路（実際は0の経路もあるけれども表示されない）があるので、制約を与えるターゲットをどのように選ぶかが複雑でしたが、要約すれば以下のような感じになります。

・ターゲットとなる部分巡回路もしくは足し合わせた都市群の数は全体都市数の半数未満とする

・分離した部分巡回路あるいは都市群がある場合は、その都市群がターゲット

・分離した部分巡回路がない場合は、0.5の部分巡回路とそれに付随する1.0の部分経路を足し合わせた都市群をターゲットとする

・足し合わせた都市群が他の都市群と接続している箇所が、２未満の場合は２以上の制約をあたえる

・足し合わせた都市群が他の都市群と接続している箇所が、３以上の場合は２以下の制約をあたえる

この条件分けで繰り返しループ処理させるコードが以下になります。

def st_elim(ST10, ST05, ST15):
    st_flat = None
    if len(ST15) > 1:
        st_flat = set(sum(ST15[0], ()))
    else:
        if len(ST15[0]) == num:#  and is_loop(ST15[0]):
            st_flat = set(sum(ST15[0], ()))
            print('Optimal')
        else:
            if len(ST05) > 0:
                for st05 in ST05:
                    st05f = set(sum(st05, ()))
                    for st10 in ST10:
                        st10f = set(sum(st10, ()))
                        if len(st05f & st10f) >= 2 and len(st05f | st10f) < num / 2:
                            st05f |= st10f
                            st_flat = st05f

    print('st:',st_flat)
    return st_flat

while True:
    E10 = [e[i] for i, x in enumerate(res.x) if x > 0.99]
    E05 = [e[i] for i, x in enumerate(res.x) if x > 0.49 and x <= 0.51]
    E15 = E10 + E05
    
    ST10 = subtour_list(E10)
    ST05 = subtour_list(E05)
    ST15 = subtour_list(E15)
    
    st_flat = st_elim(ST10, ST05, ST15)
    
    if st_flat == set(range(num)):
        print('Optimal')
        draw_plot(False, E10, E05)
        break
         
    if st_flat is None:
        print('st_flat is None')
        break
    else:            
        cnt = 0
        for i, j in E10:
            if len({i, j} & st_flat) == 1:
                cnt += 1
            
        if cnt > 2:
            A_ub.append([1 if len({i, j} & st_flat) == 1 else 0 for (i, j) in e])
            b_ub.append(2)
            #print('cnt:', cnt)
        else:
            A_ub.append([-1 if len({i, j} & st_flat) == 1 else 0 for (i, j) in e])
            b_ub.append(-2)
        res = linprog(c=dist, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds, method="revised simplex")

最初のst_elim()というのが、ターゲットとなる都市群を探し出す関数です。そして続くwhileループ内でターゲットとなる都市群に条件（他都市との接続数）に応じて制約を追加していきます。今回の場合1ループで約10秒、48都市を解決するのに約2分かかりました。

他のサンプルでは試していないので、まだ完璧ではないかもしれませんが（これから検証）、一応scipyを用いて試してみたという感じです。

関連：TSP: Traveling Salesman Problem / 巡回セールスマン問題について

以下が全体のコード：