自作CNCマシン・レーザーカッターについて: クロス積

ラベル クロス積 の投稿を表示しています。すべての投稿を表示

2021年4月7日水曜日

IK（逆運動学）：同次変換行列、クロス積によるヤコビ行列（その２）

今回は、同次変換行列やクロス積を使って、2Dロボットアームの動きを逆運動学で求めてみます（前回はこちら）。

環境：Python3.8.5、Jupyter Notebook

＊numpy.matrix()は将来的に削除されるのでnumpy.array()を使用しています。

＊尚、コーディングにおいての行列の掛け算（ドット積）は：

A・B = numpy.dot(A, B) = A.dot(B) = A @ B

今回試す内容：

同次変換行列を用いる
ヤコビ行列をクロス積（外積）で求める
任意のリンク数に対応させる（以下画像：N=20の場合）

同次変換行列（FK）：

各ジョイントに対応した同次変換行列を数珠つなぎに掛け合わせることで各端点のベクトルが簡単に求められます。2Dなので3x3マトリクスでも足りるのですが、後々の3Dのために4x4マトリクスを使うことにします。

前回までは、ジョイント1の回転角をθ1とすればジョイント2の回転角はθ1+θ2としていましたが、今回の場合は単純に相対角度であるθ2だけ入力すればいいので計算しやすくなります。

2Dにおける同次変換行列をHとすれば、

H = [[cos(θ), -sin(θ), 0, x],
     [sin(θ),  cos(θ), 0, y],
     [     0,       0, 1, 0],
     [     0,       0, 0, 1]]

3Dでは左上3x3が回転用、右端3x1が平行移動用ですが、今回のような2Dロボットアームであれば、xにリンク長、y=0を代入して以下のようになります。

H = [[cos(θ), -sin(θ), 0, L],
     [sin(θ),  cos(θ), 0, 0],
     [     0,       0, 1, 0],
     [     0,       0, 0, 1]]

HをLとθを引数とした関数にすれば、3リンクアームの場合、

V = H(0,θ1)・H(L1,θ2)・H(L2,θ3)・[L3,0,0,1].T

によってV=[x,y,0,1].Tが求まり、(x, y)を取り出せばアーム先端（End-Effector）の2Dベクトルになります。

コーディングでは以下のような感じ。

def H(L, TH):
    return np.array([[np.cos(TH), - np.sin(TH), 0, L],
                     [np.sin(TH),   np.cos(TH), 0, 0],
                     [         0,            0, 1, 0],
                     [         0,            0, 0, 1]])

L  = [1, 1, 1]
TH = np.radians([30, 30, 30])
EE = np.array([[L[2], 0, 0, 1]])
V = H(0, TH[0]) @ H(L[0], TH[1]) @ H(L[1], TH[2]) @ EE.T
print(V)

最後に掛けているEE.Tは、End-Effectorのベクトルです。@はドット積。

そうすると、出力は以下。

[[1.3660254]
 [2.3660254]
 [0.       ]
 [1.       ]]

4x1行列の上２行がEnd-Effectorのベクトル(x, y)になります。

前述のコーディングでは、ジョイントの数だけH(L, TH)を掛け合わせましたが、実際はfor文で繰り返し処理します。

クロス積でヤコビ行列を求める：

運動学は同次変換行列によって求められたので、次に逆運動学の下準備としてヤコビ行列を求めます。前回は、運動学によって求まるEnd-Effector座標のxとy成分の計算式を各ジョイントの回転角θ1、θ2、θ3によって偏微分しました（以下）。

J(Θ) = [[- L1sin(θ1) - L2sin(θ1+θ2) - L3sin(θ1+θ2+θ3), - L2sin(θ1+θ2) - L3sin(θ1+θ2+θ3), - L3sin(θ1+θ2+θ3)],
        [  L1cos(θ1) + L2cos(θ1+θ2) + L3cos(θ1+θ2+θ3),   L2cos(θ1+θ2) + L3cos(θ1+θ2+θ3),   L3cos(θ1+θ2+θ3)]]

今回はクロス積によってこのヤコビ行列を求めます。

ジョイントの回転軸の単位ベクトル（Z軸ベクトル[0,0,1]）を求める。
各回転軸からEnd-Effectorまでのベクトルを求める。
この２つのベクトルをクロス積で掛け合わせx、yの変化率（速度）を求める
ith_J = [0, 0, 1] × (End_Effector_vector - ith_Joint_vector)

×はクロス積。クロス積は、XY平面上の２つのベクトルによってできる平行四辺形の面積をXY平面に直行するZ軸方向のベクトルとして表します（以下）。

A×B = |A||B|sin(θ)[0,0,1]

ちなみにドット積は（以下）、

A・B = |A||B|cos(θ)

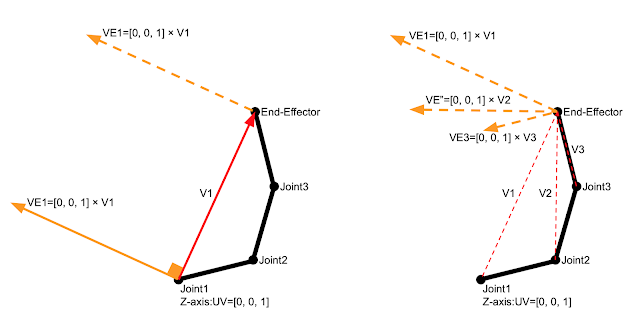
左図：

Joint1を回転軸とする場合、Joint1からEnd-EffectorまでのベクトルをV1、Z軸の単位ベクトル[0, 0, 1]をUV、End-Effectorの回転速度VE1とすると、

UV = [0, 0, 1]
V1 = End_Effector_vector - Joint1_vector
VE1 = UV × V1

になります。

Z軸の単位ベクトル[0, 0, 1]にV1をクロス積で掛け合わせると、「右ねじの法則」によってV1に直行する黄色実線のベクトルが得られます。また、End-Effectorにおける回転速度はV1に対して垂直な黄色破線として表され、これも同様に[0, 0, 1] × V1で表すことができます。

要はEnd-Effectorの速度ベクトルVE1は、V1を90度反時計回りに回転させたベクトルと同じになります。あるいは、End-Effectorにおける接線に沿ったベクトル（V1のx成分とy成分を-1倍したものを入れ替えたベクトル）になります。V1の角度をθ_v1とすれば以下。

V1  = [ |V1|cos(θ_v1), |V1|sin(θ_v1)]
VE1 = [-|V1|sin(θ_v1), |V1|cos(θ_v1)]

右図：

同様に、Joint2からEnd-EffectorまでのベクトルをV2、Joint3からEnd-EffectorまでのベクトルをV3とすれば、それぞれの回転軸で回転させたときのEnd-Effectorの接線方向の速度ベクトルが求まります。これで、V1、V2、V3の速度の割合が求まります。

V1、V2、V3は速度ベクトルなので、プログラム上では任意にスケールダウンして、1ループあたりの移動変化量を調整できます。

クロス積を用いた場合は、偏微分も各ジョイントにおける角度も必要なく、単なるベクトルだけの計算になるためシンプルです。

UV  = [0, 0, 1]
VE1 = UV × V1 = [- |V1|sin(θ_v1), |V1|cos(θ_v1), 0]
VE2 = UV × V2 = [- |V2|sin(θ_v2), |V2|cos(θ_v2), 0]
VE3 = UV × V3 = [- |V3|sin(θ_v3), |V3|cos(θ_v3), 0]

よってヤコビ行列Jは、

J = [UV × V1, UV × V2, UV × V3]

実際は1列にｘ，ｙ，ｚの３要素が含まれているため、3xNの行列になります（Nはリンク数）。

コードでは以下。

def Jacobian(V):
    UV = np.array([0, 0, 1])
    J = []
    for i in range(N):
        J.append(np.cross(UV, V[:, -1] - V[:, i]))
    return np.array(J).T

Vは各ジョイントのベクトルで、V[:, -1]はEnd-Effectorのベクトル、V[:, i]は回転軸となるジョイントのベクトル。

IK（逆運動学）：

今回は任意のリンク数に対応できるように、同次変換行列Hをfor文で繰り返しFK()という運動学の関数に組み込んでおきます。

def H(L, TH):
    return np.array([[np.cos(TH), - np.sin(TH), 0, L],
                     [np.sin(TH),   np.cos(TH), 0, 0],
                     [         0,            0, 1, 0],
                     [         0,            0, 0, 1]])

def FK(L, TH):
    N = len(L)
    T = H(0, TH[0])
    V = np.zeros(3)
    for i in range(N-1):
        T = T @ H(L[i], TH[i+1])
        V = np.c_[V, T[:3, -1]]
    EE = T @ np.array([[L[-1], 0, 0, 1]]).T
    V = np.c_[V, EE[:3, -1]]
    return V

ヤコビ行列の疑似逆行列は前回同様numpy.linalg.pinv(J)で求めることにします。

ちなみに疑似逆行列は、pinv(J)=J.T ・(J・J.T)^-1。

while True:
    V = FK(L, TH)
    J = Jacobian(V)
    Error = Target - V[:, -1]
    if norm(Error) < 1e-4:
        break
    dTheta = pinv(J) @ Error * scaler
    TH += dTheta

4行目のV[:, -1]はEnd-Effectorのベクトルで、Target=[x,y,z]との差分をErrorとして疑似逆行列と掛け合わせています（＠はドット積）。scalerは刻み幅を細かくするための係数（scaler=0.1〜0.01程度）。

結果的にΔθ：dThetaが求まり、dThetaを現在の角度THに加算してTargetに近づいていきます。誤差が0.0001未満になったらループ終了。

コード：

変数Nでリンク数を増やすことができます。
インタラクティブモード（アームをマウスに追従させる）があるためbackendは%matplotlib notebookにしてあります。