前回までは2Dアームでしたが、今回は3Dアームにおける逆運動学です。
環境:Python3.8.5、Jupyter Notebook
これまでの2Dアーム逆運動学:
- Inverse Kinematics 逆運動学:Backward Shift、FABRIK、CCD
- Jacobian Inverse Kinematics :ヤコビ行列を用いた逆運動学(その1)
- IK(逆運動学):同次変換行列、クロス積によるヤコビ行列(その2)
- IK(逆運動学):アーム可動域制限(角度制限)CCDとFABRIKの場合
- IK(逆運動学):同次変換行列/ヤコビ行列(クロス積)/角度制限
- IK(逆運動学):複数の円の交点から求める
- 左上:3D表示
- 右上:真上からの視点(X-Y平面)
- 右下:正面からの視点(X-Z平面)
- 赤い×は目標座標
- Joint0[0,0,0]はZ軸を中心にLink0(Joint1)を回転させる
- Joint1[0,0,0.5]はY軸を中心にLink1(Joint2)を回転させる
- Joint2[1,0,0]はY軸を中心にLink2(Joint3)を回転させる
- Joint3[1,0,0]はY軸を中心にLink3(End-Effector)を回転させる
同次変換行列:
def H(axis, vec, theta):
if axis == 'X':
return np.array([[1, 0, 0, vec[0]],
[0, cos(theta), -sin(theta), vec[1]],
[0, sin(theta), cos(theta), vec[2]],
[0, 0, 0, 1]])
elif axis == 'Y':
return np.array([[cos(theta), 0, -sin(theta), vec[0]],
[ 0, 1, 0, vec[1]],
[sin(theta), 0, cos(theta), vec[2]],
[ 0, 0, 0, 1]])
elif axis == 'Z':
return np.array([[cos(theta), -sin(theta), 0, vec[0]],
[sin(theta), cos(theta), 0, vec[1]],
[ 0, 0, 1, vec[2]],
[ 0, 0, 0, 1]])
else:
return np.array([[1, 0, 0, vec[0]],
[0, 1, 0, vec[0]],
[0, 0, 1, vec[0]],
[0, 0, 0, 1]])
FK(運動学):
def FK(L, TH):
N = len(L)
T = H('Z', L[0], TH[0])
V = np.array(T[:3,-1])
for i in range(1, N-1):
T = T @ H('Y', L[i], TH[i])
V = np.c_[V, T[:3,-1]]
EE = T @ np.array([[1,0,0,1]]).T
V = np.c_[V, EE[:3, -1]]
return V
T = H('Z', [0,0,0], 0) @ H('X', [0,0,0.5], pi/2) @ H('X', [1,0,0], 0) @ H('X', [1,0,0], 0) @ EE
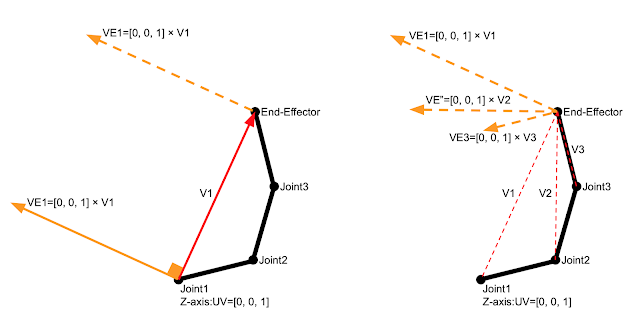
IK(逆運動学)とヤコビ行列:
角度制限:
def angleLimit(TH, MinA, MaxA):
THCOPY = TH.copy()
for i in range(len(TH)):
THCOPY[i] = TH[i] % tau
if THCOPY[i] > pi:
THCOPY[i] -= tau
if THCOPY[i] < MinA[i]:
THCOPY[i] = MinA[i]
if THCOPY[i] > MaxA[i]:
THCOPY[i] = MaxA[i]
return THCOPY
インタラクティブモード:
def click(event):
global TH, mx, my, mz
if event.inaxes == A10.axes:
mx = event.xdata
my = event.ydata
elif event.inaxes == A20.axes:
mx = event.xdata
mz = event.ydata
else:
pass
# 以下省略