Tensorflowもあっというまに1.9までバージョンアップしており、トップページが日本語表示になっていました。Get started with Tensorflowという最初のチュートリアルも変わったようで、Keras、Eager、EstimatorがHigh Level APIとして前面にでてきています。Pytorchも試していましたが、Tensorflowがますます便利になっていくのでTensorflowに戻りつつあります。書きやすくなったEagerやtf.layersも試してみましたが、結局Kerasがシンプルでわかりやすいという結論に達し、Keras自体もバージョンアップしたようなのでTensorflowというよりもKerasでVAEを試してみようかと。
VAEは中間層で突然正規分布が登場して、ベイズ的な手法で画像生成していくアルゴリズムが興味深く、固定値を確率に変換して表現するという部分がずっと気になっていました(
最初に試したのは約10ヶ月前)。
潜在空間、ベイズ推定、Reparameterization trick、KL-divergenceなど、画像生成に通じるテクニックを勉強するにはちょうどいいサンプルだと思います(かなり難しいですが)。
TensorflowでKerasをインポートする際に、以前はtensorflow.python.kerasだったけど、Tensorflow 1.9からは、tensorflow.kerasで使えるようになったようです。
Kerasの書き方:
Kerasの場合いくつか書き方があり、
Sequential()の中に各層をそのまま並べて行く方法。
model = Sequential([
Dense(32, input_shape=(784,)),
Activation('relu'),
Dense(10),
Activation('softmax'),
])
Sequential()でモデルを定義してから各層をaddで追加していく方法。
model = Sequential()
model.add(Dense(32, input_shape=(784,))
model.add(Activation('relu'))
model.add(Dense(10))
model.add(Activation('softmax'))
これらの方法はSequentialモデルと呼ばれ、各層をそのまま重ねていけばいいのでわかりやすい。
このほか、functional APIというモデルがあり、各層に変数をつけて行末の()に前の層を代入し、最後にモデルを定義する方法。
inputs = Inputs(shape=(784,))
layer1 = Dense(32, activation='relu')(inputs)
outputs = Dense(10, activation='softmax')(layer1)
model = Model(inputs,outputs)
行末の()なしで各層を連結させないで書くには以下。あとから連結式(代入式)を書いて、先ほどの結果(Model)と同じになります。
inputs = Inputs(shape=(784,))
l1 = Dense(32, activation='relu')
l2 = Dense(10, activation='softmax')
layer1 = l1(inputs)
outputs = l2(layer1)
model = Model(inputs,outputs)
Sequentialモデルのほうがすっきりしてわかりやすいけれども、VAEの場合だと少し複雑になるので、今回はfunctional APIで各層を別々に書いていくタイプを使います。
そのほか、これらModelクラスをサブクラス化する書き方もあるけれど、一行ずつ順を追ってベタに書いていったほうが理解しやすいので、今回はサブクラス化せずにJupyter Notebookに書いていこうと思います。
VAEの実装:
環境:
Ubuntu 18.04
GTX 1060
CUDA 9.0
python 3.6
tensorflow 1.9
Jupyter Notebook 5.6
まずは各モジュールのインポート。
import tensorflow as tf
from tensorflow.keras.models import Model
from tensorflow.keras import losses, backend as K
from tensorflow.keras.layers import Dense, Input, Lambda
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
そして、今回使用するmnistデータセットの読み込みと正規化、28x28の画像を784の1次元へ平坦化。
mnist = tf.keras.datasets.mnist
(x_train, y_train),(x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
x_train = x_train.reshape(60000, 784)
x_test = x_test.reshape(10000, 784)
このへんはサンプルなどでもお馴染みの方法。
Encoderと潜在変数z:
そして、encoder層。
# encoder
inputs = Input(shape=(784,))
encoder_h = Dense(256, activation='relu')(inputs)
z_mu = Dense(2, activation='linear')(encoder_h)
z_log_sigma = Dense(2, activation='linear')(encoder_h)
encoderは、784次元に平坦化された画像を入力とし、reluを通して256次元に変換、その後さらに2次元へ変換し正規分布のパラメータとなる平均muと分散logΣに分けておきます。分散をΣではなくlogΣにしているのは、encoderからの出力が負の場合もあるため、Σ=σ
2が常に正であるのに対し、logをつけることで負の値であっても成立するようにしているらしい(
論文p11でもlogσ
2と書いてある)。
要は、計算から求められる固定値を正規分布という確率分布に置換してから演算することで画像生成を可能にしているようです。
平均と分散をもとに正規分布から値を取り出すには通常サンプリング(ある確率に従ってランダムに値を取り出す)が必要となり、数式では以下のようにあらわします。
z~N(μ,Σ)
このサンプリング式をnumpyであらわすと、
z=np.random.normal(loc=μ, scale=Σ, size=1)
になりzを求めることは可能ですが、サンプリングすると後々バックプロパゲーションが不可能(微分不可能)となるため、
Reparameterization trickという代替演算法をつかうようで、
z=μ+Σ
0.5*ε
に置き換えて(平均値μに誤差εを掛け合わせた分散Σを足し合わせるという感じ)、
上の式中のΣをlogΣに変換するには、
Σ=exp(logΣ)
であるから、最終的には、
z=μ+exp(0.5*logΣ)*ε
という式になるようです。この部分が以下のdef sampling()の内容です。
def sampling(args):
z_mu, z_log_sigma = args
epsilon = K.random_normal(shape=(K.shape(z_mu)[0], K.int_shape(z_mu)[1]))
return z_mu + K.exp(0.5 * z_log_sigma) * epsilon
z = Lambda(sampling)([z_mu, z_log_sigma])
# encoder model
encoder = Model(inputs, [z_mu, z_log_sigma, z])
encoder.summary()
潜在変数zを求めるLambda(keras.layers.Lambdaクラス)の部分はKerasのモデルの一部に組み込むために必要で、そのままsampling()関数からの戻り値を受け取るだけだと、モデルの一部としてバックプロパゲーションなどしてくれなくなるようです。
最後にsummary()でこのモデルの各層を確認できます(以下)。
_______________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) (None, 784) 0
__________________________________________________________________________________________________
dense (Dense) (None, 256) 200960 input_1[0][0]
__________________________________________________________________________________________________
dense_1 (Dense) (None, 2) 514 dense[0][0]
__________________________________________________________________________________________________
dense_2 (Dense) (None, 2) 514 dense[0][0]
__________________________________________________________________________________________________
lambda (Lambda) (None, 2) 0 dense_1[0][0]
dense_2[0][0]
==================================================================================================
Total params: 201,988
Trainable params: 201,988
Non-trainable params:
先程のLambdaの計算部分もモデルに組み込まれているのがわかります。最初pythonのlambda式と勘違いしており意味がわかりませんでしたが、これはKerasレイヤーのLambdaということです。
Decoder:
そして残りのdecoder層。decoder層は訓練用と画像生成用の2種類のモデルをつくっておきます。これは訓練用の方です。
# decoder
d_h = Dense(256, activation='relu')
d_out = Dense(784, activation='sigmoid')
decoder_h = d_h(z)
outputs = d_out(decoder_h)
# vae: encoder + decoder
vae = Model(inputs, outputs)
vae.summary()
画像生成時にもこのレイヤーを使い回すので、それぞれのレイヤーごとに分けて書いておき、次の行でzと隠れ層を代入します。そして、encoderの入力からdecoderの出力までを足し合わせてvaeモデル(訓練用)をつくります。vae.summary()で先程と同様にモデルの各層を確認します(以下)。
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) (None, 784) 0
__________________________________________________________________________________________________
dense (Dense) (None, 256) 200960 input_1[0][0]
__________________________________________________________________________________________________
dense_1 (Dense) (None, 2) 514 dense[0][0]
__________________________________________________________________________________________________
dense_2 (Dense) (None, 2) 514 dense[0][0]
__________________________________________________________________________________________________
lambda (Lambda) (None, 2) 0 dense_1[0][0]
dense_2[0][0]
__________________________________________________________________________________________________
dense_3 (Dense) (None, 256) 768 lambda[0][0]
__________________________________________________________________________________________________
dense_4 (Dense) (None, 784) 201488 dense_3[0][0]
==================================================================================================
Total params: 404,244
Trainable params: 404,244
Non-trainable params: 0
入力784次元、256次元、2次元(z_mu, z_log_sigma, z)、256次元、784次元という各層があることがわかります。基本的にはz_muとz_log_sigmaの二つだけでいいのですが、比較もしたいためにzも組み込んでおきました。
Generator:
上記のvaeモデル(encoder+decoder)でz値を通して訓練用画像(x_train)で学習しますが、訓練後はz_muとテスト画像(x_test)を用いてpredict(予測/画像生成)します。
その画像生成する際のgeneratorのコードが以下。
# generator
generator_in = Input(shape=(2,))
generator_h = d_h(generator_in)
generator_out = d_out(generator_h)
generator = Model(generator_in, generator_out)
generator.summary()
後々使うのですが、とりあえす先につくっておきます。
Loss function:
つぎは、ロスの計算です。この部分はVAE特有の難しいアルゴリズムで、Reconstruction lossの最大化とKL-divergence loss最小化を組み合わせることになりますが論文や解説などを参考にするしかないと言う感じ。KL-divergenceは二つの分布の比較の値を計算してくれるようです。差が少ないほど0に近づくので最小化していくには便利。
ネットで探してみるとKerasのバージョンによっても違いがあるのか計算方法や関数が微妙に異なっており、いろいろ試した結果この方法に(
参考はここ)。recon内で784を掛けていますがK.sum()でもいいのかもしれません。
def vae_loss(inputs, outputs):
recon = 784 * losses.binary_crossentropy(inputs, outputs)
kl = - 0.5 * K.sum(1 + z_log_sigma - K.square(z_mu) - K.exp(z_log_sigma), axis=-1)
return K.mean(recon + kl)
vae.compile(optimizer='adam', loss=vae_loss)
epochs = 10
vaefit = vae.fit(x_train, x_train,
shuffle=True,
epochs=epochs,
batch_size=64,
validation_data=(x_test, x_test),
callbacks=[])
今回はadamで最適化してみました。vae.fit()内のcallbacks=[]を加えることで訓練中のロス値を呼び出すことができるようで、それを利用してグラフを描くことができるようです。Tensorboardも利用できるようですが、今回はmatplotlibで。
# plot loss
loss = vaefit.history['loss']
val_loss = vaefit.history['val_loss']
plt.plot(range(1,epochs), loss[1:], marker='.', label='loss')
plt.plot(range(1,epochs), val_loss[1:], marker='.', label='val_loss')
plt.legend(loc='best', fontsize=10)
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
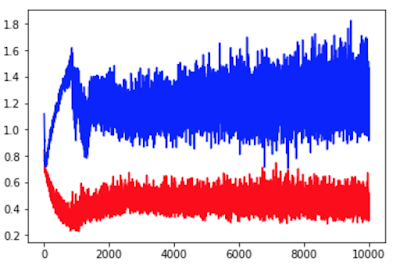
このコードを書き加えると以下のグラフが描けます。
100エポック回したときのロスの変化です。まだ下がりそうですが、100エポックでやめてしまいました。GTX1060で1エポック3秒前後(batch_size=64)。
隠れ層のユニット数やbatch_sizeを調整したほうがいいのかもしれませんが続行。
視覚化:
つぎは、結果の出力。
hidden_imgs = encoder.predict(x_test)
model_imgs = generator.predict(hidden_imgs[0])
vae_imgs = vae.predict(x_test)
s = 0
n = 10
plt.figure(figsize=(10, 3.1))
plt.subplots_adjust(wspace=0, hspace=0)
for i in range(n):
#original
ax = plt.subplot(3, n, i + 1)
plt.imshow(x_test[i+s].reshape(28, 28))
plt.axis('off')
plt.gray()
#reconstruction
ax = plt.subplot(3, n, i + 1 + n)
plt.imshow(model_imgs[i+s].reshape(28, 28))
plt.axis('off')
#vae model
ax = plt.subplot(3, n, i + 1 + n + n)
plt.imshow(vae_imgs[i+s].reshape(28, 28))
plt.axis('off')
plt.show()
最初にencoder層をpredictし、その結果(hidden_imgs[0]はz_muによる出力)をgenarator層(生成用モデル)に渡して画像を得ています。同様にvae(訓練用モデル)も使って画像生成してみました(こちらはz経由での出力)。
結果の画像。オリジナル、encoder/z_mu/generator生成画像、vaeモデル:encoder/z/decoder生成画像。
4と9のような画像が多いので、まだ改良の余地がありそうです。
そして、2次元の潜在空間(z_mu)での各数字の分布。二つの値がそれぞれ横軸と縦軸に割り当てられそれを座標上に表したものです。
plt.figure(figsize=(10,10))
plt.scatter(hidden_imgs[0][:,0] ,hidden_imgs[0][:,1], marker='.', c=y_test, cmap=plt.get_cmap('tab10'))
plt.colorbar()
plt.grid()
cmapでtab10を用いることで10段階で色分けしています。結果の画像は以下。
これを見ると数字の5(茶色)が、かろうじてy=0より少し上に横に細長く並んでいるのがわかります。0、1、3、7は、領域がはっきり分かれているため認識しやすそうですが、それ以外は中央に重なるように集中しているので識別しにくそうです。
さらに、この分布をグリッド状の画像に置き換えるコード。
n = 20
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
grid_x = np.linspace(-2, 2, n)
grid_y = np.linspace(-2, 2, n)[::-1]
for i, yi in enumerate(grid_y):
for j, xi in enumerate(grid_x):
z_sample = np.array([[xi, yi]])
x_decoded = generator.predict(z_sample)
digit = x_decoded[0].reshape(digit_size, digit_size)
figure[i * digit_size: (i + 1) * digit_size, j * digit_size: (j + 1) * digit_size] = digit
plt.figure(figsize=(10, 10))
start_range = digit_size // 2
end_range = n * digit_size + start_range + 1
pixel_range = np.arange(start_range, end_range, digit_size)
sample_range_x = np.round(grid_x, 1)
sample_range_y = np.round(grid_y, 1)
plt.xticks(pixel_range, sample_range_x)
plt.yticks(pixel_range, sample_range_y)
plt.xlabel("z [0]")
plt.ylabel("z [1]")
#plt.imshow(figure, cmap='gnuplot')
plt.imshow(figure, cmap='Greys_r')
plt.show()
先程の分布のグラフはx:-4〜4、y:-4〜4の範囲ですが、このコード内の4、5行目のgrid_xとgrid_yのnp.linspaceの範囲を-2〜2に変えることで、その範囲での数の分布を見ることができます。以下がその結果。
これは分布グラフの範囲をx:-2,2、y:-2,2に限定して出力したものです。先程のドットの分布で5が水平に細長く分布していたように、この画像においても中央右寄りに細長く水平に分布しています。一応一通り0〜9が存在していますが、分布領域が広範囲な数と狭い範囲にしかない数があるのがわかります。
ただ、このような結果から1と3と5の中間に8が位置していたりと、その特性を利用して面白い画像生成ができそうです。
まとめ:
VAEは以前Tensorflowのサンプルを試しましたが、単なるAutoencoderに比べると潜在変数やReparameterization trick、さらにはロス関数の部分の理解が難しいという印象でした。今回あらためてKerasで書いてみると、Kerasのシンプルな構造のおかげか、かなり理解が深まりました。特に最後の2つの分布的なグラフについてはどう表示するのかと思っていましたが、どこをいじればどうなるかが分かりました。
通常のAutoencoderの場合なら入力から出力までそのまま層を重ねて行けばいいのですが、VAEの場合だと中間層で正規分布からサンプリングするため、そのままだと訓練時にバックプロパゲーションができなくなってしまうことからReparameterization trickで微分計算可能な経路につくりかえます。訓練後はReparameterization trickは必要ないので、encoderからそのまま分布の中心位置となるz_mu経由でgeneratorを通り出力するということになっています。
訓練時(x_train):
encoder
z_mu, z_log_sigma
z(Reparameterization trick)
decoder
訓練後(x_test):
encoder
z_mu
generator
参考にしたサイト:
https://qiita.com/kenchin110100/items/7ceb5b8e8b21c551d69a
https://wiseodd.github.io/techblog/2016/12/10/variational-autoencoder/
https://www.kaggle.com/rvislaywade/visualizing-mnist-using-a-variational-autoencoder
https://blog.csdn.net/A_a_ron/article/details/79004163
関連:
tf.kerasでDCGAN(Deep Convolutional Generative Adversarial Networks)
Posted with
Amakuri at 2018.12.21
Antonio Gulli, Sujit Pal
オライリージャパン
販売価格 ¥3,672