クォータニオンは主に3DCG内のオブジェクトの回転制御で使われています。通常のXYZ軸ごとの角度制御よりも便利らしい。
しかしながら、二次元を複素平面で表現したように、三次元空間を四元数(一つの実数と三つの虚数i、j、k)によって表現しようとしている部分も興味深い。
クォータニオンは、
Q = w + x*i + y*j + z*k (i2=j2=k2=ijk=-1)
で表現され、wは実数で残りの三つはXYZ軸に対応した複素数のようなもの。
Pythonにおいてはijkはないので、4つに分解して、
Q = [w, x, y, z]
という配列で表現しています。
回転制御:
通常回転制御する場合は、XYZ軸を何度ずつ動かせばいいのかと考えますが、クォータニオンの場合は回転軸一つと角度一つだけで制御します。
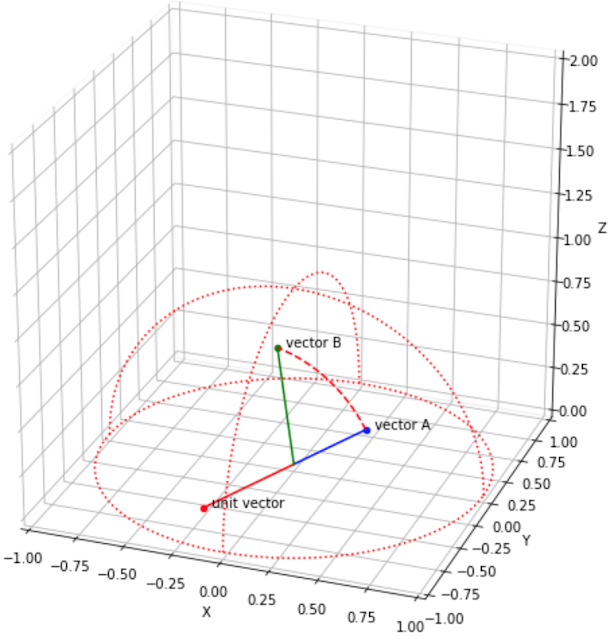
まず青いA点が単位球面上にあり、赤い回転軸(単位ベクトル:unit vector)を45度回すとBにたどり着くという状況があります。
この時点で、
・Aのベクトル(XYZ座標)
・回転軸(unit vector)のベクトル(XYZ座標)
・回転角(45度)
はすでに与えられており、この操作をするとBのベクトル(XYZ座標値)が得られるということになります。
言い換えれば、この操作方法によってAがどこに向かうのかを知りたいのであって、AからBにいくための操作方法を知りたいということではないので、きっかけが異なるとこの部分で少し戸惑います(AとBの二点間の回転移動を逆算して単位ベクトルと回転角度を求める内容は次回)。
しかしながら、赤い回転軸があれば単位球面上を最短距離でBに辿りつくことができます。わざわざ、X軸に何度、Z軸に何度、Y軸に何度と角度を三つに分解しなくても一つの角度だけで実現できるメリットがあり回転ツールとしては便利です。ただし3点はすべて単位曲面上にあるのでスカラー(半径)は1で座標値がそのままベクトルになります。
これをクォータニオンで計算するには、Aのベクトル[x, y, z]をクォータニオン式に変換し(wを付け足すだけ、w=0)、
A = [w, x, y, z]
とし、回転軸(unit vector)はベクトルのまま、
U = [ux, uy, uz]
として、クォータニオンの回転制御の公式である
w, x, y, z = Q*A*Q-
にいれれば、到着点であるBのベクトル/座標値[x, y, z]がわかります。
ただ、この公式の中身(QとQ-)が少し複雑です。
Q = [cos(θ/2), ux*sin(θ/2), uy*sin(θ/2), uy*sin(θ/2)] Q- = [cos(θ/2), -ux*sin(θ/2), -uy*sin(θ/2), -uy*sin(θ/2)]
上式のθに回転角、回転軸:単位ベクトルのux, uy, uz値を代入。尚、Q-はQの共役クォータニオンで式中にマイナスがついており、Q*Q-=1という関係となっています。
さらに、クォータニオンの掛け算では各XYZにijkの虚数が含まれているため、実部wと虚部ijkの項に分けて計算します。
q1*q2 = [[q1w*q2w - q1x*q2x - q1y*q2y - q1z*q2z],
[q1w*q2x + q1x*q2w + q1y*q2z - q1z*q2y],
[q1w*q2y - q1x*q2z + q1y*q2w + q1z*q2x],
[q1w*q2z + q1x*q2y - q1y*q2x + q1z*q2w]]
= [w, x, y, z]
4段ありますが、上からw, x, y, z(実部, 虚部3つ)に対応しています。掛け算の結果として、[w, x, y, z]が得られるので、このうち[x, y, z]だけを取り出せばベクトル(XYZ座標値)になります。
また、ベクトル、内積、外積を使えばもう少し式が短くなります。
q1*q2: w = q1w * q2w - (v1・v2)
x, y, z = q1w * v2 + q2w * v1 + (v1×v2)
1段目が実部wに対応しており、2段目の虚部の式はXYZに対応した三つの値を返すので、そのままベクトルとして使えます。尚、(v1・v2)の部分はドット積(numpy.dot(v1, v2))、また(v1× v2)の部分はクロス積(numpy.cross(v1, v2))。ちなみに、v1=[q1x, q1y, q1z]はq1=[q1w, q1x, q1y, q1z]のXYZ成分です。
掛け算は複雑そうですが、コーディングする場合は一度関数にしておいて代入するだけなので楽です。
角度は一つしか登場してこないのでアニメーションなどつくるときには便利そうです。
ベクトルの正規化:
ベクトル[x, y, z]に実部wを加えればクォータニオンの式になりますが、先ほどの計算は全て正規化されていないとだめなので元のベクトルをスカラー値で割って正規化しておきます。
A = [x, y, z]
の場合、
√(x2 + y2 + z2) = 1
にならなければいけないので(ノルム:1)、
A_normalized = [x, y, z] / √(x2 + y2 + z2)
となります。実際Pythonではリストの割り算は一気にできないので、
A_normalized = np.array([x, y, z]) / ((x**2 + y**2 + z**2))**0.5
= np.array(A) / np.linalg.norm(A)
になります。
同様にクォータニオンの場合は、
√(w2 + x2 + y2 + z2) = 1
でなければならないので、
Q = np.array([w, x, y, z]) / ((w**2 + x**2 + y**2 + z**2))**0.5
になります。
スカラー値で割って正規化して計算し、結果のベクトルを求め、それをスカラー倍すれば元のスケールに戻ります。
計算手順:
計算手順を再度まとめると、
A = [ax, ay, az] (これから動かそうとする点)
An = A / |A| (正規化)
U = [ux, uy, uz] (単位ベクトル:回転軸)
Un = U / |U| (正規化が必要であればしておく)
t = θ (回転角)
以上が予め決めておくこと。
以下の式に角度と単位ベクトル(回転軸ベクトル)を代入しておきます。
Q = [cos(t/2), ux*sin(t/2), uy*sin(t/2), uy*sin(t/2)] Q- = [cos(t/2), -ux*sin(t/2), -uy*sin(t/2), -uy*sin(t/2)]
そして、回転の公式で求めます。
w, x, y, z = Q*A*Q- (QにAを掛けて、その結果にQ-を掛ける)
上式クォータニオン同志の掛け算は、以下の式を利用。
q1*q2 = [[q1w*q2w - q1x*q2x - q1y*q2y - q1z*q2z],
[q1w*q2x + q1x*q2w + q1y*q2z - q1z*q2y],
[q1w*q2y - q1x*q2z + q1y*q2w + q1z*q2x],
[q1w*q2z + q1x*q2y - q1y*q2x + q1z*q2w]]
= [w, x, y, z]
結果として[w, x, y, z]が求まるので、XYZ成分だけを取り出してベクトルにします。
[x, y, z] (回転後のベクトル:単位球面上でのXYZ座標)
正規化される前のベクトルと同等のスカラー値に戻したい場合は、元のスカラー値を掛け直します。
[x, y, z] * |A| (スカラー倍で元のスケールにする)
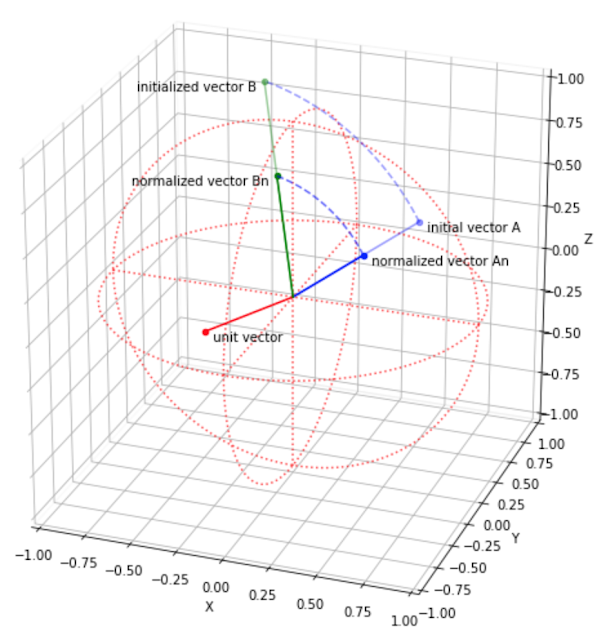
手順:
・まず、initial vector Aを正規化してnormalized vector Anにします。
・normalized vector Anをunit vector(回転軸)で45度回転させます。
・回転後はnormalized vector Bnが得られます。
・normalized vector BnにAのスカラー値をかけるとinitialized vector Bになります。
・よって、AからBに移動したことになります。
以下がPython(Jupyter Notebook)コード:
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D %matplotlib inline
A = np.array([1, -1, 1]) # initial vector A (arbitary vector) As = np.linalg.norm(A) # scalar of A: |A| An = A / As # normalization: should be (sum(x**2 + y**2 + z**2))**0.5 = 1.0 U = np.array([-0.1, -0.9, 0.2]) # unit vector (not normalized) Us = np.linalg.norm(U) # scalar of U: |U| UV = U / Us # unit vector (normalized) # quaternion multiplication function def QbyQ(q1, q2): # q = [w, x, y, z] w = q1[0]*q2[0] - q1[1]*q2[1] - q1[2]*q2[2] - q1[3]*q2[3] i = q1[0]*q2[1] + q1[1]*q2[0] + q1[2]*q2[3] - q1[3]*q2[2] j = q1[0]*q2[2] - q1[1]*q2[3] + q1[2]*q2[0] + q1[3]*q2[1] k = q1[0]*q2[3] + q1[1]*q2[2] - q1[2]*q2[1] + q1[3]*q2[0] return np.array([w, i, j, k]) # quaternion rotation function def QPQc(P, UV, t): # P: quaternion, UV: unit vector, t: rotation angle theta q = [np.cos(t/2), UV[0] * np.sin(t/2), UV[1] * np.sin(t/2), UV[2] * np.sin(t/2)] qc = [np.cos(t/2), -UV[0] * np.sin(t/2), -UV[1] * np.sin(t/2), -UV[2] * np.sin(t/2)] qP = QbyQ(q, P) result = QbyQ(qP, qc) return result QA = np.insert(An, 0, 0) # quaternion of An: [0, x, y, z] theta = np.deg2rad(45) # rotation angle QB = QPQc(QA, UV, theta) # quaternion rotation for An with UV and theta Bn = QB[1:] # vectorize the quaternion result B = Bn * As # new vector as same scalar as initial vector A上記のプロット:
def plot_base(elev=25, azim=-70): fig = plt.figure(figsize=(10, 10)) ax = fig.add_subplot(111, projection='3d') ax.view_init(elev=elev, azim=azim) ax.set(xlim=(-1, 1), ylim=(-1 ,1), zlim=(-1, 1)) ax.set(xlabel='X', ylabel='Y', zlabel='Z') ax.xaxis.pane.fill = ax.yaxis.pane.fill = ax.zaxis.pane.fill = False t = np.linspace(0, 2*np.pi, 128+1) alpha = 0.7 ax.plot(np.cos(t), np.sin(t), [0]*len(t), linestyle=':', c='red', alpha=alpha) ax.plot(np.cos(t), [0]*len(t), np.sin(t), linestyle=':', c='red', alpha=alpha) ax.plot([0]*len(t), np.cos(t), np.sin(t), linestyle=':', c='red', alpha=alpha) ax.plot([-1, 1], [0, 0], [0, 0], linestyle=':', c='red', alpha=alpha) ax.plot([0, 0], [-1, 1], [0, 0], linestyle=':', c='red', alpha=alpha) ax.plot([0, 0], [0, 0], [-1, 1], linestyle=':', c='red', alpha=alpha) return ax ax = plot_base() ax.plot([0, A[0]], [0, A[1]], [0, A[2]], c='b', alpha=0.4) # vector A ax.scatter(A[0], A[1], A[2], c='b', alpha=0.4) ax.text(A[0], A[1], A[2], s=' initial vector A', va='top') ax.plot([0, An[0]], [0, An[1]], [0, An[2]], c='b') # vector A normalized ax.scatter(An[0], An[1], An[2], c='b') ax.text(An[0], An[1], An[2], s=' normalized vector An', va='top') ax.plot([0, UV[0]], [0, UV[1]], [0, UV[2]], c='r') # unit vector ax.scatter(UV[0], UV[1], UV[2], c='r') ax.text(UV[0], UV[1], UV[2], s=' unit vector', va='top') ax.plot([0, B[0]], [0, B[1]], [0, B[2]], c='g', alpha=0.4) # vector B ax.text(B[0], B[1], B[2], s='initialized vector B ', ha='right', va='top') ax.scatter(B[0], B[1], B[2], c='g', alpha=0.4) ax.plot([0, Bn[0]], [0, Bn[1]], [0, Bn[2]], c='g') # vector B normalized ax.scatter(Bn[0], Bn[1], Bn[2], c='g') ax.text(Bn[0], Bn[1], Bn[2], s='normalized vector Bn ', ha='right', va='top') Arc = [QPQc(QA, UV, t) for t in np.linspace(0, theta, 33)] # arc between A and B arw, arx, ary, arz = np.array(Arc).T ax.plot(arx, ary, arz, linestyle='--', c='b', alpha=0.6) ax.plot(arx*As, ary*As, arz*As, linestyle='--', c='b', alpha=0.4)
まとめ:
クォータニオンの回転制御の公式に従えば簡単に操作できることがわかりました。それよりも3Dグラフに補助線を引いたりするコーディングのほうが大変でした。回転操作の計算内訳は少々複雑ですが、一旦ファンクション化してしまえば、あとは代入するだけなので手順はシンプルです。回転制御だけでなく、四元数そのものも気になります。
次回は、少し疑問に思っていた二点間の回転移動を逆算してみようと思います。
関連:
クォータニオン / 回転制御(その2):二点間から単位ベクトルと回転角度を求める
クォータニオン / Quaternion:立方体の回転操作(その3)
























