前回に引き続きクォータニオン回転制御についてです。
今回は任意の二点(ベクトルAとB)だけが与られていて、AからBへ回転移動する際に必要な単位ベクトルと回転角度を求めてみます。
しかしながら、任意の二点(AとB)といっても、いくつかのケースがあります。
(1)AとBが単位球面上に存在する(|A|=|B|=1のとき)
(2)AとBのスカラー値は同じだけど、単位球面上に存在しない(|A|=|B|≠1のとき)
(3)AとBのスカラー値が異なり、単位球面上に存在しない(|A|≠|B|≠1)
(
4)そもそもAもBも単位ベクトルには無関係な任意の2点の場合
*(4)に関しては、AからBへの直線移動も含まれるし、単位ベクトル自体も任意に決定できるので今回は省略。このことから、任意の二点といってもあくまで単位球を設定しなければ逆算できないということがわかります。
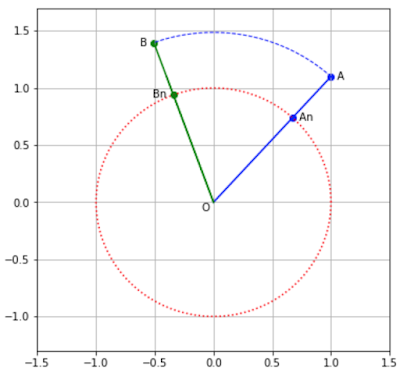
(1)と(2)の場合(AとBのスカラー値が等しい場合):
(1)が一番簡単で、(2)も回転操作後に(1)の値を元のスカラー倍すればいいので、回転操作自体は同じ計算方法になります。以下はXZ平面において回転軸Yの場合。
単純にAが回転するとBになったという状況。回転操作のためには一旦ベクトルAを正規化してAnにしなければならないので、AnからBnへの回転計算をしたのち、正規化されているBnを元のスカラー倍してBとなります。
単位ベクトルを求める:
この場合、単位ベクトル(UV)は正規化されたAnとBnがあればクロス積(外積)で求めることができます(単位ベクトル(UV)は、ベクトルAnとベクトルBnに対して垂直/法線ベクトルとなるため)。ただし、Aのスカラー値とBのスカラー値は等しいという前提です(|A|=|B|)。
Pythonであれば、
A = [ax, ay, ax] # ベクトルA
B = [bx, by, bz] # ベクトルB
As = np.linalg.norm(A) # Aのスカラー値
Bs = np.linalg.norm(B) # Bのスカラー値 ただしAs=Bsという前提
An = np.array(A) / As # 正規化
Bn = np.array(B) / Bs # 正規化
UV = np.cross(An, Bn) # 求められた単位ベクトル
回転角度を求める:
またAB間の回転角度(theta)はドット積(内積)とarccos()で求められ、
cos_AnBn = np.dot(An, Bn)
theta = np.arccos(cos_AnBn)
この二つの値(UV、theta)をクォータニオンの回転公式に代入し、Anを回転すれば計算結果がBnと一致します。そして正規化するまえの大きさに戻すため元のスカラー倍(Aのスカラー)します。
コード:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
# quaternion multiplication function
def QbyQ(q1, q2): # q = [w, x, y, z]
w = q1[0]*q2[0] - q1[1]*q2[1] - q1[2]*q2[2] - q1[3]*q2[3]
i = q1[0]*q2[1] + q1[1]*q2[0] + q1[2]*q2[3] - q1[3]*q2[2]
j = q1[0]*q2[2] - q1[1]*q2[3] + q1[2]*q2[0] + q1[3]*q2[1]
k = q1[0]*q2[3] + q1[1]*q2[2] - q1[2]*q2[1] + q1[3]*q2[0]
return np.array([w, i, j, k])
# quaternion rotation function
def QPQc(P, UV, t): # P: quaternion, UV: unit vector, t: rotation angle theta
q = [np.cos(t/2), UV[0] * np.sin(t/2), UV[1] * np.sin(t/2), UV[2] * np.sin(t/2)]
qc = [np.cos(t/2), -UV[0] * np.sin(t/2), -UV[1] * np.sin(t/2), -UV[2] * np.sin(t/2)]
qP = QbyQ(q, P)
result = QbyQ(qP, qc)
return result
# find unit vector and rotation angle for two vectors A and B
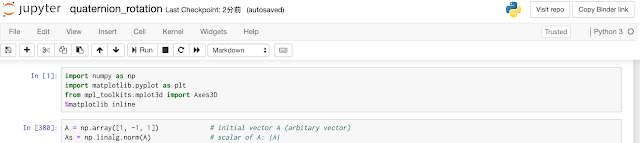
A = np.array([1, -1, 0.2]) # start point A
As = np.linalg.norm(A) # scalar of A: |A|
An = A / As # normalization
B = np.array([0.4, -0.1, 1.1]) # end point B
Bs = np.linalg.norm(B) # scalar of B: |B|
Bn = B / Bs # normalization
# find unit vector for An-Bn rotation
AnxBn = np.cross(An, Bn) # orthogonal vector to An-Bn
UV = AnxBn / np.linalg.norm(AnxBn) # unit vector (normalized): rotation axis
# find rotation angle about An-Bn
# cos_t = (An dot Bb) / (|An|*|Bn|) # (|An|*|Bn|) = An * Bn = 1 * 1 = 1
cos_AnBn = np.dot(An, Bn)
theta_AnBn = np.arccos(cos_AnBn) # angle between An and Bn
# reproduct A-B rotation
Qa = np.insert(An, 0, 0) # quaternion of An: [0, x, y, z]
Qb = QPQc(Qa, UV, theta_AnBn) # quaternion rotation for An with UV and theta_AB
Bn_new = Qb[1:] # new Bn vector (normalized): [bx, by, bz]
B_new = Bn_new * Bs # new B vector
print('unit vector:', UV)
print('theta (degrees):', np.rad2deg(theta_AnBn))
print('initial vector B:', B)
print('new vector B :', B_new)
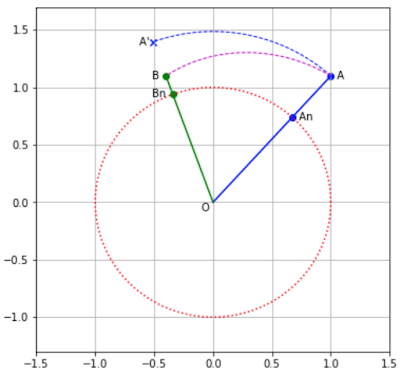
(3)の場合(AとBのスカラー値が異なる場合):
しかし(3)の場合は、単位球に対する任意の二点ABということから、Aを単純に回転させた結果がBになるとは限りません。以下のような状況。
Aを単純に回転させればA'(×印)にたどり着きますが、AとBのスカラー値(半径)が異なる場合はピンクの破線のような動きになります。Aは回転しつつ半径も縮まっていくという変化。
この場合、回転操作は(1)と同様に正規化されたベクトルAnで行い、最終的にAn(Bnと同じ)をBのスカラー倍(Bs倍)すればいいことになります。
回転軸となる単位ベクトルは(1)と同様にAnとBnのクロス積で求まります。
A = [ax, ay, ax] # ベクトルA
B = [bx, by, bz] # ベクトルB
As = np.linalg.norm(A) # Aのスカラー値
Bs = np.linalg.norm(B) # Bのスカラー値
An = np.array(A) / As
Bn = np.array(B) / Bs
UV = np.cross(An, Bn) # 求められた単位ベクトル
AnとBnの回転角度に関しても(1)と同様にドット積とarccos()で求めます。
cos_AnBn = np.dot(An, Bn)
theta_AnBn = np.arccos(cos_AnBn)
求めた単位ベクトルUV(回転軸)とtheta_AnBn(回転角度)をクォータニオンの公式に代入すればBnが求まります。求めたBnに対して元のスカラー値Bsを掛ければBになります。
しかし、これでは移動前と移動後の二つの場面しかないので、途中の軌跡を描いて滑らかに移動しているかどうか確かめてみる必要がありそうです。つまり、先程の図のAからBへの移り変わり(ピンクの破線)を描いてみるというわけです。
AからBへの移動の中間補間:
まず移動のステップ数を決め、ステップ数に応じた回転角度とAからBへのスカラー値の変化量を決めます。
steps = 33
theta = np.linspace(0, theta_AnBn, steps)
ABs = np.lispace(As, Bs, steps)
これで、回転角度thetaは33ステップで0からtheta_AnBnまで変化します。同様にAB間のスカラー値ABsの変化も33ステップでAsからBsへ変化します。あとは公式に代入して33ステップ分の結果を得ます。
arw, arx, ary, arz = np.array([QPQc(Qa, UV, t) for t in theta]).T
上式で求まるのはAn-Bn間の回転結果(角度は違うけれどもスカラー値はどれも1)なので、各ステップに応じたスカラー値の変化量ABsを掛け合わせます。
ABx = arx * ABs
ABy = ary * ABs
ABz = arz * ABs
これで、各ステップごとに正規化されたベクトルに対して段階的にスカラー倍することになります。
ipywidgetsでインタラクティブ表示:
今回も
ipywidgetsでインタラクティブなグラフを表示してみます(ブログ上ではインタラクティブに動きませんが、
mybinder.orgでこちらの
gist URLを入力すればオンライン上でも動きます)。
関連:
Binder:オンライン上でのJupyter Notebook(ipynbファイル)の実行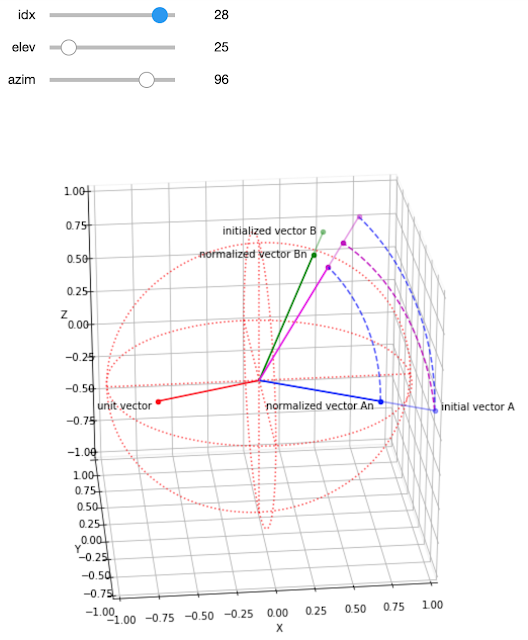
右端initial vector A(青)がinitialized vector B(緑)へ向かって移動する状態(ピンク)。unit vector:単位ベクトル(赤)が回転軸。
正規化されたAn-Bn間の回転移動は単位球面上にあります。AからBへの移動(ピンク破線)は単位球の同心円とずれているのがわかります。
クォータニオンの回転では、比較的簡単なパラメーターの調整だけで回転操作できることがわかりました。特にこのような移動途中の軌跡を描く際には便利なツールだと思います。
コード:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
# quaternion multiplication function
def QbyQ(q1, q2): # q = [w, x, y, z]
w = q1[0]*q2[0] - q1[1]*q2[1] - q1[2]*q2[2] - q1[3]*q2[3]
i = q1[0]*q2[1] + q1[1]*q2[0] + q1[2]*q2[3] - q1[3]*q2[2]
j = q1[0]*q2[2] - q1[1]*q2[3] + q1[2]*q2[0] + q1[3]*q2[1]
k = q1[0]*q2[3] + q1[1]*q2[2] - q1[2]*q2[1] + q1[3]*q2[0]
return np.array([w, i, j, k])
# quaternion rotation function
def QPQc(P, UV, t): # P: quaternion, UV: unit vector, t: rotation angle theta
q = [np.cos(t/2), UV[0] * np.sin(t/2), UV[1] * np.sin(t/2), UV[2] * np.sin(t/2)]
qc = [np.cos(t/2), -UV[0] * np.sin(t/2), -UV[1] * np.sin(t/2), -UV[2] * np.sin(t/2)]
qP = QbyQ(q, P)
result = QbyQ(qP, qc)
return result
def plot_base(elev=25, azim=-70):
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
ax.view_init(elev=elev, azim=azim)
ax.set(xlim=(-1, 1), ylim=(-1 ,1), zlim=(-1, 1))
ax.set(xlabel='X', ylabel='Y', zlabel='Z')
ax.xaxis.pane.fill = ax.yaxis.pane.fill = ax.zaxis.pane.fill = False
t = np.linspace(0, 2*np.pi, 128+1)
alpha = 0.7
ax.plot(np.cos(t), np.sin(t), [0]*len(t), linestyle=':', c='red', alpha=alpha)
ax.plot(np.cos(t), [0]*len(t), np.sin(t), linestyle=':', c='red', alpha=alpha)
ax.plot([0]*len(t), np.cos(t), np.sin(t), linestyle=':', c='red', alpha=alpha)
ax.plot([-1, 1], [0, 0], [0, 0], linestyle=':', c='red', alpha=alpha)
ax.plot([0, 0], [-1, 1], [0, 0], linestyle=':', c='red', alpha=alpha)
ax.plot([0, 0], [0, 0], [-1, 1], linestyle=':', c='red', alpha=alpha)
return ax
# find unit vector and rotation angle for two vectors A and B
A = np.array([1, -1, 0.2]) # start point A
As = np.linalg.norm(A) # scalar of A: |A|
An = A / As # normalization
B = np.array([0.4, -0.1, 1.1]) # end point B
Bs = np.linalg.norm(B) # scalar of B: |B|
Bn = B / Bs # normalization
# find unit vector for An-Bn rotation
AnxBn = np.cross(An, Bn) # orthogonal vector to An-Bn
UV = AnxBn / np.linalg.norm(AnxBn) # unit vector (normalized): rotation axis
# find rotation angle about An-Bn
# cos_t = (An dot Bb) / (|An|*|Bn|) # (|An|*|Bn|) = An * Bn = 1 * 1 = 1
cos_AnBn = np.dot(An, Bn)
theta_AnBn = np.arccos(cos_AnBn) # angle between An and Bn
# reproduct A-B rotation
Qa = np.insert(An, 0, 0) # quaternion of An: [0, x, y, z]
Qb = QPQc(Qa, UV, theta_AnBn) # quaternion rotation for An with UV and theta_AB
Bn_new = Qb[1:] # new Bn vector (normalized): [bx, by, bz]
B_new = Bn_new * Bs # new B vector
# interactive plot with ipywidgets
from ipywidgets import interact
steps = 33
Arc = np.array([QPQc(Qa, UV, t) for t in np.linspace(0, theta_AnBn, steps)]).T # arc An-Bn
_, arx, ary, arz = Arc
ABs = np.linspace(As, Bs, steps) # scalar transition from A to B
ABx = arx * ABs # x term for arc A-B
ABy = ary * ABs # y term for arc A-B
ABz = arz * ABs # z term for arc A-B
@interact(idx=(0, steps-1, 1), elev=(0, 180, 1), azim=(-180, 180, 1))
def two_vec(idx=10, elev=25, azim=96):
ax = plot_base(elev, -azim)
ax.plot([0, A[0]], [0, A[1]], [0, A[2]], c='b', alpha=0.4) # vector A
ax.scatter(A[0], A[1], A[2], c='b', alpha=0.4) # point A
ax.text(A[0], A[1], A[2], s=' initial vector A')
ax.plot([0, An[0]], [0, An[1]], [0, An[2]], c='b') # vector An
ax.scatter(An[0], An[1], An[2], c='b') # point An
ax.text(An[0], An[1], An[2], s='normalized vector An ', ha='right', va='top')
ax.plot([0, UV[0]], [0, UV[1]], [0, UV[2]], c='r') # unit vector
ax.scatter(UV[0], UV[1], UV[2], c='r')
ax.text(UV[0], UV[1], UV[2], s='unit vector ', ha='right', va='top')
ax.plot([0, B[0]], [0, B[1]], [0, B[2]], c='g', alpha=0.4) # vector B
ax.text(B[0], B[1], B[2], s='initialized vector B ', ha='right', va='center')
ax.scatter(B[0], B[1], B[2], c='g', alpha=0.4) # vector B
ax.plot([0, Bn[0]], [0, Bn[1]], [0, Bn[2]], c='g') # vector Bn
ax.scatter(Bn[0], Bn[1], Bn[2], c='g') # vector Bn
ax.text(Bn[0], Bn[1], Bn[2], s='normalized vector Bn ', ha='right', va='center')
ax.plot([0, arx[idx]], [0, ary[idx]], [0, arz[idx]], color='magenta') # vector An (move)
ax.plot([0, arx[idx]*As], [0, ary[idx]*As], [0, arz[idx]*As], c='m', alpha=0.4) # move A (move)
ax.scatter(arx[idx]*As, ary[idx]*As, arz[idx]*As, c='m', alpha=0.4) # point A (move)
ax.scatter(arx[idx], ary[idx], arz[idx], c='m') # point An (move)
ax.plot(arx[:idx+1], ary[:idx+1], arz[:idx+1], linestyle='--', c='b', alpha=0.7) # arc An-Bn
ax.plot(arx[:idx+1]*As, ary[:idx+1]*As, arz[:idx+1]*As, ls='--', c='b', alpha=0.7) # arc A-A
rate = As + (Bs - As) * idx / steps
ax.scatter(arx[idx]*rate, ary[idx]*rate, arz[idx]*rate, c='m') # point A-B
ax.plot(ABx[:idx+1], ABy[:idx+1], ABz[:idx+1], ls='--', c='m', alpha=0.9) # arc A-B
関連:
クォータニオン(四元数) / Quaternion / 回転制御(その1)
クォータニオン / Quaternion:立方体の回転操作(その3)
今野 紀雄
森北出版
売り上げランキング: 67,351
















![PythonユーザのためのJupyter[実践]入門](https://images-fe.ssl-images-amazon.com/images/I/51ZeYjBnmfL._SL160_.jpg)